Microsoft Research Asia stellt mit rStar-Math eine mehrstufige Trainingsmethode vor, mit der kleine Sprachmodelle (Small Language Models, SLMs) mit nur 1,5 bis 7 Milliarden Parametern die Leistung von OpenAIs o1-preview bei mathematischen Aufgaben erreichen oder sogar übertreffen können.
Kernstück des Trainings ist die Monte Carlo Tree Search (MCTS), eine durch AlphaGo bekannt gewordene Technik zur systematischen Erkundung von Lösungswegen. MCTS ermöglicht es dem System, während der Ausführung verschiedene Lösungspfade durchzuspielen und aus den erfolgreichsten zu lernen.
Eine zentrale Innovation von rStar-Math ist die Kombination von natürlichsprachlichen Erklärungen mit ausführbarem Python-Code. Für jeden Lösungsschritt muss das Modell nicht nur seine Gedankengänge erklären, sondern diese auch als funktionierenden Code formulieren.
Die Forscher nennen diese Technik "Code-augmentierte Chain-of-Thought": Die mathematischen Konzepte werden parallel in natürlicher Sprache und Python-Code ausgedrückt, wobei der Code als Kommentare die Erklärungen enthält. Nur Schritte, deren Code sich erfolgreich ausführen lässt, werden akzeptiert - eine Art automatische Qualitätskontrolle, die Fehler und Halluzinationen verhindern soll.
Diese strikte Verifikation durch Code-Ausführung ist gleichzeitig Stärke und Limitation: Der Ansatz funktioniert hervorragend bei mathematischen Textaufgaben, lässt sich aber nur schwer auf andere Bereiche übertragen. Bei geometrischen Aufgaben mit visuellen Komponenten oder in Domänen ohne eindeutige, programmierbare Lösungen wie dem Textverständnis stößt das System an seine Grenzen.
Die Forscher sehen jedoch Potential für die Anwendung bei Programmieraufgaben oder logischen Schlussfolgerungen, wo ähnliche Verifikationsmechanismen möglich wären.
Selbstverbesserung durch Bewertung und Evolution
Das Herzstück von rStar-Math ist ein spezielles Bewertungsmodell (Process Preference Model, PPM), das die Qualität einzelner Lösungsschritte einschätzt. Es analysiert die Ergebnisse zahlreicher MCTS-Durchläufe und vergibt "Q-Werte": Je häufiger ein Schritt zu einer korrekten Lösung führt, desto höher sein Wert. Statt absolute Bewertungen vorzunehmen, lernt das Modell durch den Vergleich von Lösungspaaren, erfolgreiche von weniger erfolgreichen Ansätzen zu unterscheiden.
Das Training erfolgt in vier Runden, beginnend mit einem Datensatz von 747.000 mathematischen Textaufgaben. In jeder Runde verbessern sich sowohl das Lösungsmodell als auch das Bewertungsmodell: Das System generiert mit MCTS schrittweise verifizierte Lösungen, die dann als Trainingsmaterial für die nächste Generation der Modelle dienen.
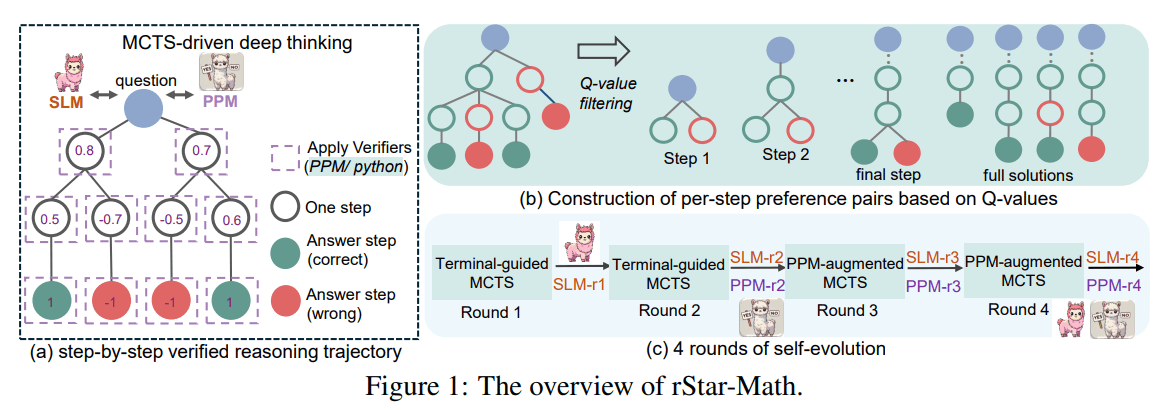
So kann das LLM mit jeder Runde komplexere Aufgaben lösen und die Qualität der erzeugten Lösungen steigt. Im Gegensatz zu anderen Ansätzen lernt das System aus seinen eigenen besten Lösungen, anstatt auf vorgegebene Musterlösungen großer Sprachmodelle angewiesen zu sein.
Spitzenleistungen in einem engen Feld
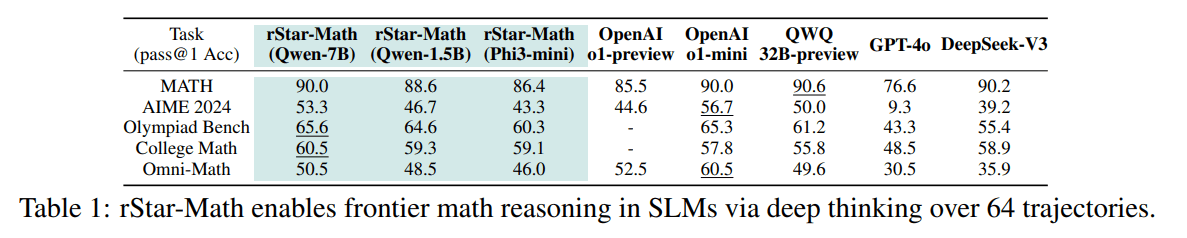
Das 7-Milliarden-Parameter-Modell Qwen2.5-Math-7B erreichte nach dem Training mit rStar-Math im MATH-Benchmark eine Genauigkeit von 90 Prozent - eine Verbesserung von mehr als 30 Prozentpunkten gegenüber der Basisversion und 4,5 Prozent besser als OpenAIs o1-preview, auf Augenhöhe mit o1-mini. Selbst das kleinste getestete Modell Qwen-1.5B mit nur 1,5 Milliarden Parametern erreichte eine Genauigkeit von 88,6 Prozent.
Bei der amerikanischen Mathematikolympiade AIME 2024 löste das System durchschnittlich 8 von 15 Aufgaben - eine Leistung auf dem Niveau der besten 20 Prozent der teilnehmenden Schülerinnen und Schüler.
Die Forscherinnen und Forscher testeten auch den Einfluss von test-time compute auf die Ergebnisse, dem neuen Skalierungsprinzip, dem auch die OpenAI o-Modelle folgen. Dabei erhält das Modell während der Ausführung mehr Zeit, um verschiedene Lösungswege durchzuspielen und zu bewerten.
Bereits mit nur vier Lösungsversuchen übertrifft rStar-Math die Leistung von o1-preview und nähert sich o1-mini an. Mit steigender Anzahl der Lösungsversuche - bis zu 64 pro Aufgabe - verbessern sich die Ergebnisse weiter.
Allerdings zeigen sich je nach Benchmark unterschiedliche Muster: Bei MATH, AIME und der Mathematik-Olympiade flacht die Verbesserung ab etwa 64 Versuchen ab. Bei College-Math-Aufgaben hingegen steigt die Erfolgsrate kontinuierlich weiter.
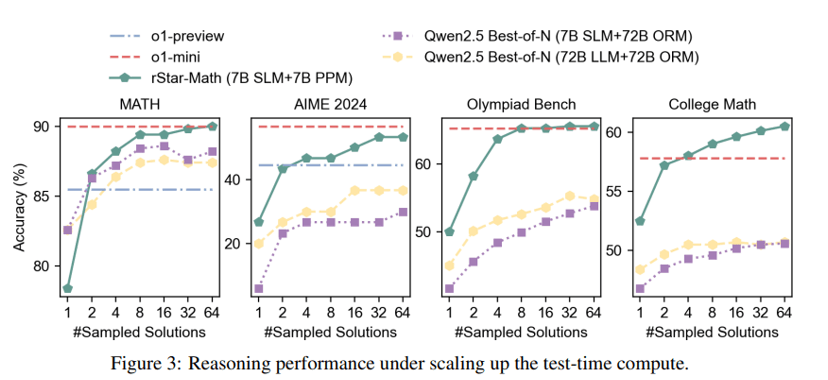
Neben der eingangs erwähnten hohen Abhängigkeit von der Code-Verifikation ist dieses Test-Time Compute-Prinzip auch ein möglicher Nachteil der Methode. Für jede Aufgabe werden Dutzende Lösungsversuche durchgeführt und ausgewertet, was zeitaufwendig und teuer ist. Die intensive Suche nach der besten Lösung ist der Preis für die hohe Genauigkeit.
Die Forscher betonen, dass rStar-Math eindrucksvoll zeigt, dass kleine Sprachmodelle eigenständig hochwertige Trainingsdaten erzeugen können, um sich selbst zu verbessern. Weitere Verbesserungen seien mit anspruchsvolleren mathematischen Aufgaben möglich.
Microsoft will KI effizienter machen
Die Entwicklung von rStar-Math ist Teil der umfassenderen Strategie von Microsoft, die Entwicklung kleinerer und effizienterer KI-Modelle voranzutreiben, um die Entwicklungs- und Betriebskosten zu senken. Erst kürzlich hatte das Unternehmen sein 14-Milliarden-Parameter-Modell Phi-4 unter der MIT-Lizenz als Open Source veröffentlicht.
Auch der Code und die Daten von rStar-Math sollen der Forschungsgemeinschaft zur Verfügung gestellt werden. Wie Projektleiterin Li Lyna Zhang auf Hugging Face mitteilt, durchläuft das Projekt derzeit noch den internen Freigabeprozess. Das Repository auf Github ist bereits angelegt, bleibt aber daher vorerst privat.
