Eine neue Studie zeigt, dass die beeindruckenden Fortschritte von Alibabas Qwen2.5-Modellen beim mathematischen Reasoning durch Reinforcement Learning hauptsächlich auf Datenkontamination zurückzuführen sind. Auf "sauberen" Benchmarks versagen dieselben Methoden.
Um die Datenkontamination zu prüfen, testeten die Forschenden, ob Qwen2.5 unvollständige Probleme vervollständigen kann. Dazu gaben sie dem Modell nur die ersten 60 Prozent einer Problemstellung aus dem MATH-500-Benchmark vor.
Das Ergebnis ist eindeutig: Qwen2.5-Math-7B rekonstruiert die fehlenden 40 Prozent mit einer Genauigkeit von 54,6 Prozent und gibt trotz der unvollständigen Problemstellung in 53,6 Prozent der Fälle die korrekte Antwort. Llama3.1-8B erreicht nur 3,8 Prozent bzw. 2,4 Prozent. Diese Fähigkeit deutet stark darauf hin, dass Qwen die Probleme bereits aus dem Training kennt.
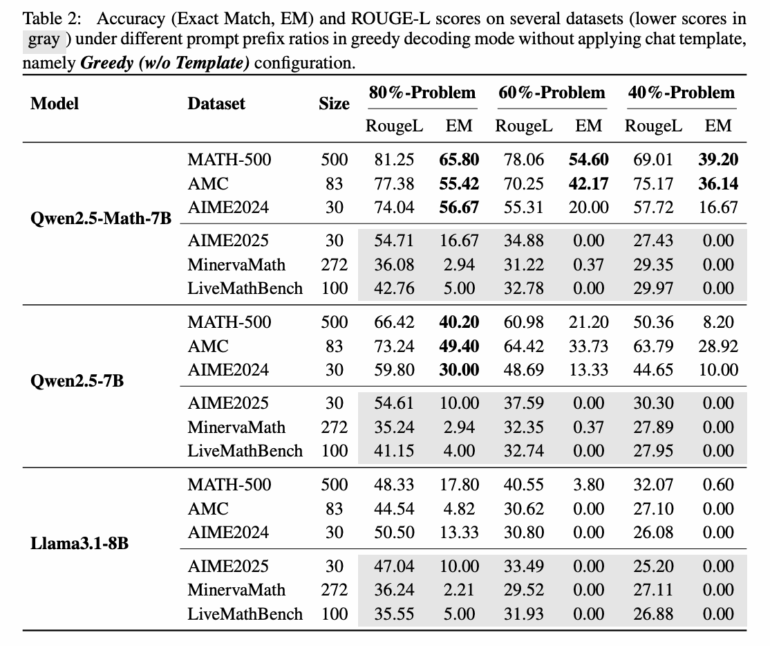
Der Verdacht bestätigt sich durch Tests mit dem erst kürzlich veröffentlichten LiveMathBench (Version 202505), der nach der Veröffentlichung von Qwen2.5 erstellt wurde. Auf diesem "sauberen" Benchmark fällt Qwens Vervollständigungsrate auf 0,0 Prozent, identisch mit Llama. Die Antwortgenauigkeit sinkt auf nur zwei Prozent.
Die Erklärung liegt wahrscheinlich im Vortraining von Qwen2.5 auf massiven webbasierten Korpora, die GitHub-Repositories mit Benchmark-Problemen und ihren offiziellen Lösungen enthalten. Besonders auffällig ist, dass selbst zufällige oder inkorrekte Belohnungssignale die Leistung von Qwen2.5-Math-7B auf MATH-500 verbessern.
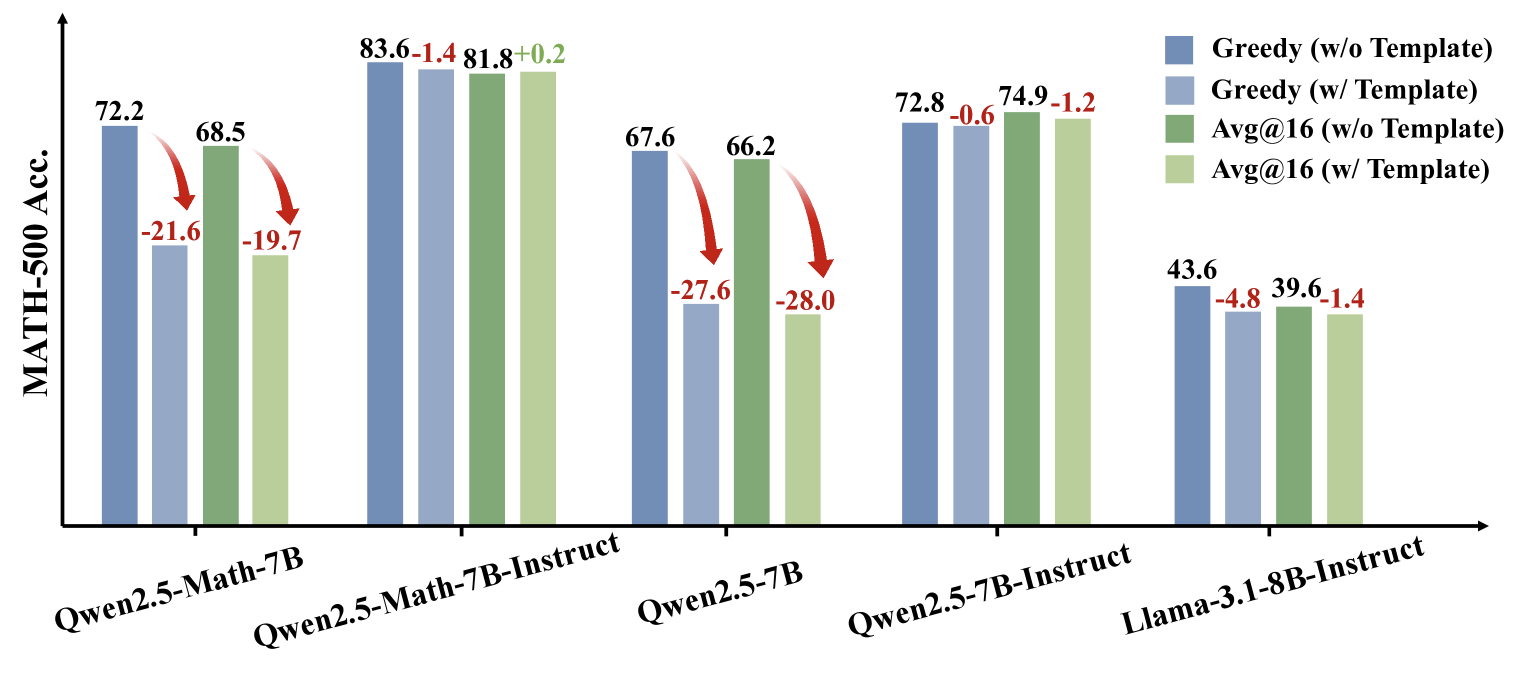
Saubere Evaluation mit synthetischen Problemen
Um ihre Hypothese zu testen, entwickelten die Forschende das RandomCalculation-Dataset mit vollständig synthetischen arithmetischen Problemen. Diese verwenden zufällige Operanden und Operatoren und wurden garantiert nach der Veröffentlichung von Qwen2.5 erstellt, wodurch Datenkontamination ausgeschlossen wird.
Auf diesem sauberen Benchmark zeigt sich ein gänzlich anderes Bild: Qwen2.5 weist eine monoton fallende Genauigkeit mit steigender Komplexität auf. Nur korrekte Belohnungssignale führen zu stabilen Verbesserungen, während zufällige Belohnungen das Training instabil machen und invertierte Belohnungen die mathematischen Fähigkeiten schnell verschlechtern.
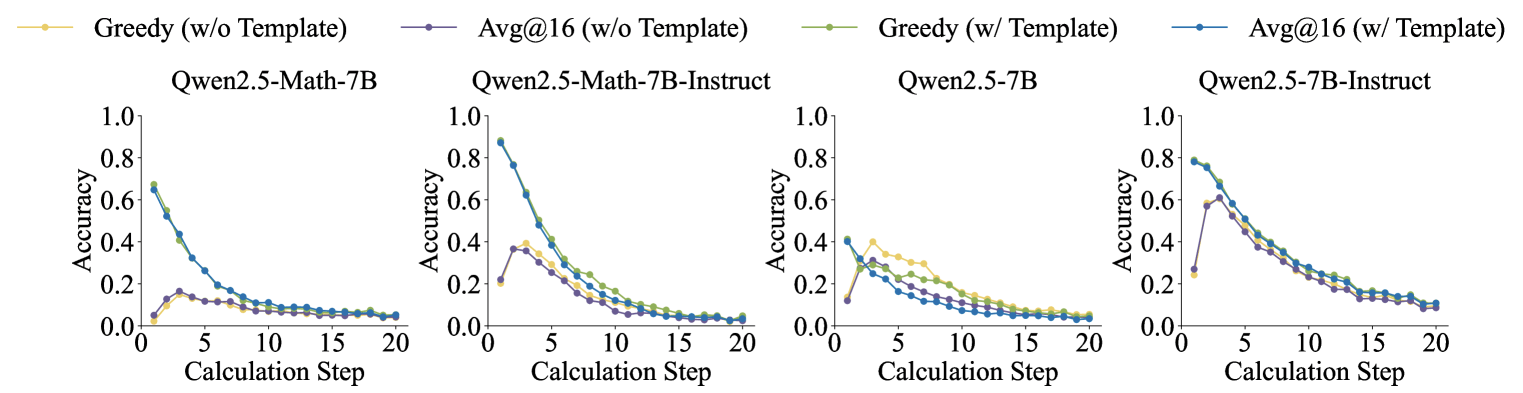
Kontrollierte Experimente bestätigen Kontamination
Die kontrollierten RLVR-Experimente (Reinforcement Learning with Verifiable Rewards) auf dem sauberen Dataset liefern eindeutige Ergebnisse:
- Korrekte Belohnungen führen zu konsistenten Leistungsverbesserungen, die die ursprüngliche Modellleistung übertreffen.
- Zufällige Belohnungen machen das Training hochgradig instabil ohne zuverlässige Verbesserungen.
- Invertierte Belohnungen verschlechtern die mathematischen Fähigkeiten des Modells rapide.
Diese Ergebnisse widerlegen die alternative Erklärung, dass Qwens überlegene mathematische Grundfähigkeiten für die scheinbaren RL-Erfolge verantwortlich sind.
Alibaba hatte Qwen2.5 im September 2024 vorgestellt und mit Qwen3 eine neue Modellfamilie eingeführt. Ob die Ergebnisse auch für Qwen3 gelten, müssen weitere Untersuchungen prüfen.
KI-Benchmarks mit begrenzter Aussagekraft
Die Studie warnt eindringlich vor der Verwendung kontaminierter Benchmarks für die Evaluation von RL-Methoden. Die Autoren empfehlen, dass zukünftige Studien auf unkontaminierten Benchmarks evaluieren und verschiedene Modellserien testen sollen.
Die Ergebnisse unterstreichen, wie schwierig es ist, echte Reasoning-Fähigkeiten von bloßer Erinnerung ("Memorization") zu unterscheiden und wie wichtig saubere Evaluationsmethoden für vertrauenswürdige KI-Forschung sind.
Schon zuvor hatten Untersuchungen demonstriert, wie wenig aussagekräftig Benchmarks unter Umständen sind. Bei Metas Llama 4 wurde nachgewiesen, dass das Unternehmen eine speziell für den LMArena-Benchmark optimierte Version eingereicht hat, die durch ausgefeilte Antwortformate bessere Bewertungen erzielte.
Andere Studien zeigen, dass Sprachmodelle wie Gemini 2.5 Pro oder Claude 3.5 Sonnet Testsituationen mit bis zu 95-prozentiger Treffsicherheit erkennen und ihr Verhalten entsprechend anpassen können, was grundlegende Fragen zur Validität von Evaluierungsverfahren aufwirft.
