Deepmind hat mit AlphaGeometry2 einen bedeutenden Fortschritt bei der automatischen Lösung von Geometrieproblemen erzielt. Das neuro-symbolische System, das einen sprachmodellbasierten KI-Agenten mit einer Symbol-Engine kombiniert, übertrifft erstmals das Niveau eines durchschnittlichen Goldmedaillengewinners der Internationalen Mathematik-Olympiade (IMO) im Fach Geometrie.
AlphaGeometry2 ist eine stark verbesserte Version des 2024 vorgestellten Systems AlphaGeometry. Es löst laut Deepmind 84 Prozent aller Geometrieprobleme der IMO aus den Jahren 2000 bis 2024, eine deutliche Steigerung gegenüber den 54 Prozent des Vorgängers.
Auf dem IMO-AG-50-Benchmark, der alle 50 Geometrieprobleme der IMO von 2000 bis 2024 umfasst, die in die AlphaGeometry-Sprache formalisiert werden konnten, löst AlphaGeometry2 42 von 50 Problemen. Damit übertrifft es einen durchschnittlichen Gold-Medaillisten, der etwa 40 von 50 Problemen löst. Das System schneidet damit laut dem Team auch deutlich besser ab als andere KI-Ansätze.
Kombination aus Sprachmodell und symbolischer Deduktion
Im Kern kombiniert AlphaGeometry2 zwei Hauptkomponenten: Ein leistungsfähiges Sprachmodell und eine symbolische Engine namens DDAR (Deductive Database Arithmetic Reasoning).
Das auf der Gemini-Architektur basierende Sprachmodell wurde auf einer großen Menge synthetischer Geometrieprobleme trainiert. Es schlägt mögliche Hilfsschritte und -konstruktionen vor, die zur Lösung eines gegebenen Problems beitragen könnten. Dazu generiert es Sätze in einer domänenspezifischen Sprache, die geometrische Objekte und Beziehungen beschreibt.
Die symbolische Engine DDAR übernimmt dann diese Vorschläge und leitet daraus weitere logische Fakten ab. Sie folgt dabei einer festen Menge von Ableitungsregeln und fügt iterativ neue Fakten hinzu, bis keine weiteren mehr abgeleitet werden können. So entsteht eine "deduktive Hülle" aller ableitbaren Fakten.
Iterativer Suchprozess mit Wissensaustausch
Der Problemlösungsprozess von AlphaGeometry2 besteht aus einer iterativen Suche. In jedem Schritt generiert das Sprachmodell eine Reihe möglicher Hilfsschritte, die dann von DDAR auf logische Konsistenz und Relevanz überprüft werden. Vielversprechende Kandidaten werden beibehalten und in der nächsten Iteration weiterverfolgt.
Ein Schlüsselelement ist dabei der neuartige Suchalgorithmus SKEST (Shared Knowledge Ensemble of Search Trees). Mehrere Suchbäume mit unterschiedlichen Strategien laufen parallel und tauschen über einen gemeinsamen Wissensspeicher vielversprechende Zwischenergebnisse aus. So können sie sich gegenseitig verstärken und die Suche beschleunigen.
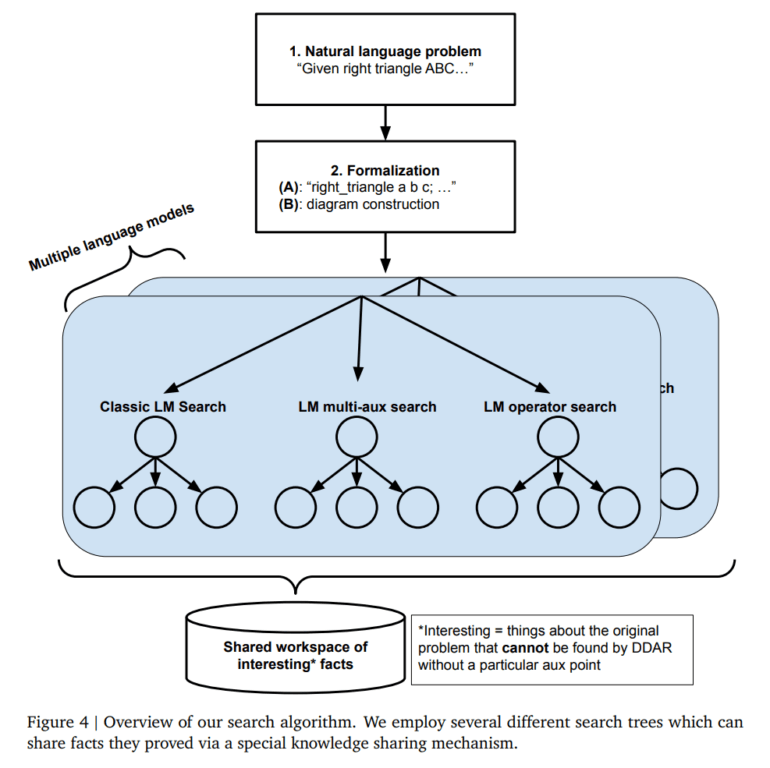
Wenn die symbolische Engine schließlich einen vollständigen Beweis gefunden hat, der vom Sprachmodell vorgeschlagene Schritte mit bekanntem Wissen verbindet, gibt AlphaGeometry2 diesen als Lösung aus. Die Beweise sind laut dem Team oft erstaunlich kreativ und elegant.
Erweiterungen und Optimierungen für mehr Leistung
Gegenüber der Vorgängerversion AlphaGeometry wurden in der neuen Version zahlreiche Erweiterungen und Optimierungen vorgenommen. Dazu gehören eine ausdrucksstärkere geometrische Beschreibungssprache, die nun auch Ortskurven und lineare Gleichungen abdeckt, sowie eine schnellere C++-Implementierung von DDAR. Die neue Version soll 300 Mal schneller sein als die bisherige Python-Implementierung.
Auch das Training des Sprachmodells wurde verbessert, unter anderem durch die Verwendung eines größeren und vielfältigeren Datensatzes. Dieser enthält nun auch Probleme vom Typ "Ortskurve" sowie eine ausgewogenere Verteilung von Aufgaben mit und ohne Hilfskonstruktionen.
Spezialisierte Tokenizer und natürliche Sprache
Überraschenderweise spielen weder der verwendete Tokenizer noch die domänenspezifische Trainingssprache eine entscheidende Rolle für die Performance von AlphaGeometry2. Ähnliche Ergebnisse wurden sowohl mit maßgeschneiderten Tokenizern mit kleinem Vokabular als auch mit generischen Large-Model-Tokenizern erzielt. Auch das Training in natürlicher Sprache führte zu vergleichbaren Ergebnissen wie das Training in einer formalen Geometriesprache.
Ein weiterer interessanter Befund ist, dass Sprachmodelle, die auf mathematischen Datensätzen vortrainiert und dann auf AlphaGeometry-Daten verfeinert wurden, etwas andere Fähigkeiten erwerben als solche, die von Grund auf neu trainiert wurden. Obwohl beide auf den gleichen Daten lernen, entwickeln sie komplementäre Stärken. Durch die Kombination dieser Modelle in einem neuen Suchalgorithmus namens SKEST (Shared Knowledge Ensemble of Search Trees) kann die Lösungsrate weiter gesteigert werden.
Neuro-symbolische KI vs. Transformer
Die Studie liefert auch wichtige Erkenntnisse über die Rolle von LLMs bei der Lösung mathematischer Probleme. Es zeigte sich laut dem Paper, dass die Modelle von AlphaGeometry2 in der Lage sind, nicht nur Hilfskonstruktionen, sondern auch vollständige Beweise zu generieren. Das deute darauf hin, dass moderne Sprachmodelle das Potenzial haben, auch ohne externe Werkzeuge wie symbolische Engines zu funktionieren.
Soweit aus der Arbeit ersichtlich wurden die verwendeten Sprachmodelle auch noch nicht als Reasoning-Modelle mit den derzeit verwendeten RL-Methoden trainiert - weitere Leistungssteigerungen sind also möglich. Es ist daher wahrscheinlich, dass die nächste Version stärker auf Reasoning-Modelle setzen wird und die Rolle der symbolischen Engine zumindest experimentell reduzieren könnte.
Das Paper zu diesem Vorzeigesystem für die Leistungsfähigkeit neuro-symbolischer KI spiegelt damit auch die zentrale Debatte der aktuellen KI-Forschung wider: Können Deep-Learning-Modelle zuverlässig schlussfolgern? Oder genauer: Können generative Transformermodelle wie LLMs lernen, zuverlässig zu schlussfolgern? Während AlphaGemeomtry2 deutlich die Stärken neuro-symbolischer Systeme zeigt, lassen die dabei vom Team gewonnen Einblicke in die Rolle von LLMs eine abschließende Antwort also weiter offen.
Einschränkungen und Use-Cases
Trotz der beeindruckenden Fortschritte hat auch AlphaGeometry2 noch Grenzen. So erlaubt die verwendete formale Sprache noch keine Beschreibung von Problemen mit variablen Punktzahlen, nichtlinearen Gleichungen oder Ungleichungen. Auch bleiben einige IMO-Aufgaben ungelöst. Mögliche Ansatzpunkte für weitere Verbesserungen sind eine Zerlegung komplexer Probleme in Teilprobleme und die Anwendung von Reinforcement Learning.
Neben Geometrieaufgaben könnte der Ansatz auch auf andere Bereiche der Mathematik und Naturwissenschaften ausgedehnt werden. Denkbar sind Anwendungen von der Lösung komplexer Berechnungen in Physik und Ingenieurwesen bis hin zur Unterstützung von Forschern und Studierenden.
Zuvor hatte Deepmind mit AlphaGo, AlphaFold und AlphaTensor bereits beeindruckende KI-Ergebnisse in den Bereichen Go, Proteinstrukturvorhersage und Matrixmultiplikation erzielt - und mit AlphaFold sogar einen Nobelpreis gewonnen.
