Die Integration des Monte Carlo Tree Search (MCTS) Algorithmus in große Sprachmodelle könnte deren Fähigkeit, komplexe mathematische Probleme zu lösen, erheblich verbessern. Erste Experimente zeigen viel versprechende Ergebnisse.
Große Sprachmodelle wie GPT-4 haben bemerkenswerte Fortschritte in der Sprachverarbeitung gemacht, kämpfen aber immer noch mit Aufgaben, die strategisches und logisches Denken erfordern. Insbesondere in der Mathematik neigen die Modelle dazu, plausibel klingende, aber faktisch falsche Antworten zu produzieren.
In einer neuen Arbeit schlagen Forschende des Shanghai Artificial Intelligence Laboratory nun vor, Sprachmodelle mit dem Algorithmus Monte Carlo Tree Search (MCTS) zu kombinieren. MCTS ist ein Werkzeug zur Entscheidungsfindung, das in der künstlichen Intelligenz für Szenarien verwendet wird, die strategische Planung erfordern, wie Spiele und komplexe Problemlösungen. Eines der bekanntesten Anwendungsbeispiele ist AlphaGo und seine Nachfolgesysteme wie AlphaZero, die regelmäßig Menschen in Brettspielen geschlagen haben. Die Kombination von Sprachmodellen und MCTS gilt seit langem als vielversprechend und wird von vielen Labors untersucht - wahrscheinlich auch von OpenAI mit Q*.
In ihrer Arbeit kombinieren die chinesischen Forscher nun die explorativen Fähigkeiten von MCTS mit den Fähigkeiten von Sprachmodellen zur Selbstverbesserung (Self-Refine) und Selbstbewertung (Self-Evaluation). Beides sind im Wesentlichen Prompting-Methoden, bei denen die Ausgaben des Sprachmodells in einem eigenen Kontextfenster überprüft werden. Für sich genommen bringen Self-Refine und Self-Evaluation oft nur geringe Verbesserungen, aber in Kombination mit MCTS können sie besser unterstützt werden. Das Ergebnis ist der MCT Self-Refine (MCTSr) Algorithmus, der die Leistung von LLMs bei komplexen mathematischen Aufgaben verbessern soll.
MCTSr kombiniert Baumsuche mit Selbstbewertung und Back-Propagation
Das MCTSr-Verfahren abstrahiert den iterativen Verfeinerungsprozess mathematischer Problemlösungen in eine Suchbaumstruktur.
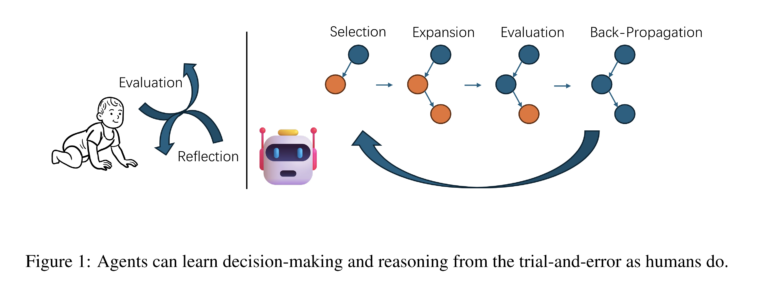
Der Algorithmus besteht aus mehreren Phasen:
- Selektion: Auswahl des vielversprechendsten Knotens zur Verfeinerung.
- Selbstverfeinerung (Self-Refine): Das LLM generiert Feedback zur Verbesserung der ausgewählten Antwort.
- Selbst-Evaluation (Self-Evaluation): Bewertung der verfeinerten Antwort durch Selbstbelohnung (Self-Reward) des LLM.
- Back-Propagation: Rückleitung der Bewertung zum Elternknoten und Aktualisierung des Baums.
- UCT-Aktualisierung: Abschließend werde neue Knoten für weitere Exploration ausgewählt.
MCTSr hebt Llama-3-8B auf GPT-4-Niveau
Die Forscher testeten MCTSr auf verschiedenen Datensätzen, darunter GSM8K, MATH und Aufgaben der Mathematik-Olympiade. In allen Fällen verbesserte sich die Erfolgsrate erheblich mit der Anzahl der MCTSr-Iterationen.
Auf dem anspruchsvollen AIME-Datensatz stieg die Lösungsrate von 2,36% im Zero-Shot-Modus auf 11,79% mit 8 MCTSr-Iterationen. Auf dem neuen GAIC Math Odyssey-Datensatz, der nach Angaben des Teams kaum Überlappungen mit den Trainingsdaten des für die Experimente verwendeten Llama-3-Modells aufweist, erreichte MCTSr eine Lösungsrate von 49,36 % gegenüber 17,22 % im Zero-Shot-Modus. Insgesamt näherte sich das verwendete Llama-3-Modell mit nur 8 Milliarden Parametern dank MCTSr damit der Leistungsfähigkeit des deutlich größeren GPT-4 an.
Das Team will die Methode nun in weiteren Anwendungsgebieten testen.
