Ein Mathematikprofessor der University of Pennsylvania hat mithilfe des KI-Modells GPT-o1-mini einen komplexen mathematischen Beweis erbracht. Der Weg dorthin war jedoch alles andere als geradlinig.
Robert Ghrist, Professor für Mathematik und Elektro- und Systemtechnik an der University of Pennsylvania, hat gemeinsam mit KI-Sprachmodellen einen mathematischen Beweis für eine Verallgemeinerung des sogenannten Bottleneck-Dualitätstheorems entwickelt. Der Prozess war laut Ghrist von "überschwänglichem Optimismus und Frustration" geprägt.
Ghrist arbeitete zunächst mit den KI-Modellen GPT-4, Claude-3.5 und Gemini-1.5-Pro zusammen. Diese konnten zwar Vermutungen aufstellen und Beweisansätze liefern, scheiterten aber immer wieder an subtilen Fehlern.
Der Durchbruch gelang schließlich mit dem neuen Modell GPT-o1-mini von OpenAI. Laut Ghrist konnte o1-mini einen fehlerhaften Beweis analysieren, die Fehler erkennen und dann innerhalb von nur 43 Sekunden einen "völlig neuen, cleveren, korrekten Beweis" generieren, der "eleganter als der menschliche Beweis" war.
Die o1-Sprachmodelle von OpenAI sind durch sogenannte Chain-of-Thoughts für logische Aufgaben optimiert und schneiden in Logik- und Planungs-Benchmarks deutlich besser ab als herkömmliche KI-Modelle, sind aber immer noch fehleranfällig.
KI-Unterstützung macht Arbeit nicht unbedingt einfacher
Ghrist betont, dass das Ergebnis "genau an der Grenze dessen liegt, was mit KI-Sprachmodellen beweisbar ist und was nicht". Das Erkennen der Fehlermodi war aus seiner Sicht entscheidend, um diese Grenze zu überschreiten.
Trotz des Erfolgs räumt Ghrist ein, dass es "schneller gewesen wäre, alles ohne KI zu machen". Die Zusammenarbeit mit den KI-Modellen habe jedoch zu einem "viel besseren" Paper geführt. Die KI habe bei den anfänglichen Vermutungen, einigen Beweisen und den meisten Anwendungen assistiert.
Das Paper enthält einen Anhang, der die Rolle und den Einfluss der KI-Sprachmodelle bei der Erstellung der Ergebnisse, Beweise und Anwendungen dokumentiert.
Der Mathematikprofessor sieht in der Erforschung der "Ecken des mathematischen latenten Raums, in denen Beweise fast funktionieren", den besten Weg, um das Potenzial künftiger KI-Modelle auszuloten. Er betont aber auch, dass es noch ein weiter Weg ist, bis KI-Modelle wirklich tiefgreifende mathematische Ergebnisse liefern können.
Menschlicher Mathematiker hat die Nase vorn
Kurz nach der Veröffentlichung wies der Mathematiker Sridhar Ramesh auf X darauf hin, dass der Beweis des Hauptresultats auch ohne KI-Unterstützung möglich gewesen wäre. Er verwies auf einen Satz von Birkhoff, der den Beweis stark vereinfache.
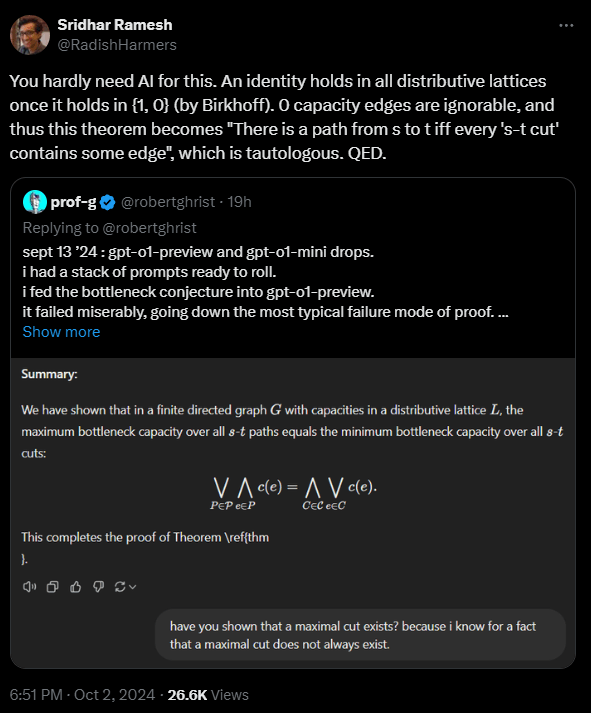
Ghrists Reaktion: "Oh! Das ist sehr cool! Ich kannte dieses Resultat nicht, und es würde die Dinge tatsächlich sehr einfach machen. Danke! Die Menschen gewinnen …"
